1 Data
Pro modelování dopadů změny klimatu bylo využito několika souborů dat, která jsou popsána v následujících kapitolách. Pro tvorbu hydrologického modelu na vybraných povodích to byla data pozorovaná (kapitola 1.1). Ta se uplatnila i při tvorbě scénářů klimatické změny, které vycházely ze simulací provedených v rámci projektů ENSEMBLES (kapitola 1.2) a CMIP5 (kapitola 1.3).
1.1 Pozorovaná data a vybraná sada povodí
Za účelem posouzení změn hydrologické bilance bylo vybráno 130 povodí a mezipovodí víceméně pokrývajících Českou republiku (viz Obr. 1.1). Definice jednotlivých povodí je součástí Přílohy P.1. Při výběru bylo vycházeno z povodí 3. řádu. V závislosti na dostupnosti pozorovaných řad byly hranice jednotlivých povodí a mezipovodí optimalizovány tak, aby zájmové jednotky měly řádově stejnou velikost, a aby existovala pozorovaná data odtoků pro kalibraci hydrologického modelu Bilan. Zejména při výpočtu odtoku z mezipovodí, kde se odtok odvozuje z rozdílů odtoků jednotlivých dílčích povodí, byla dostupnost dat značně limitujícím faktorem (více viz kapitola 2).
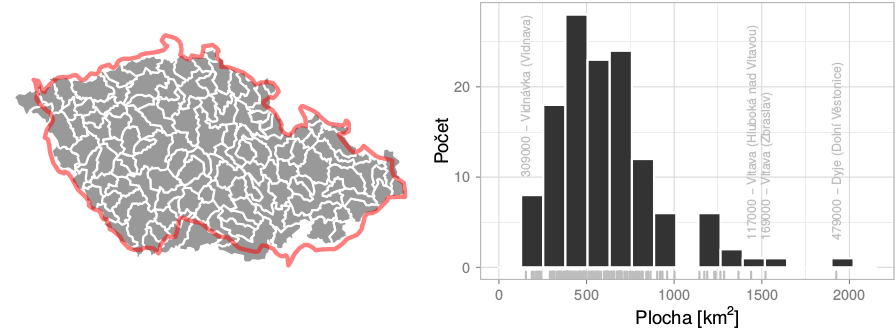
Obr.1.1 Vybraná sada povodí (vlevo) a jejich rozloha (vpravo).
Kromě měsíčních odtokových řad byly pro kalibraci hydrologického modelu Bilan dále použity měsíční časové řady srážek a teploty pro období 1961–2010. Tyto řady byly odvozeny z datasetu gridovaných srážek a teploty v rozlišení 25 km × 25 km (Štěpánek et al. 2011). Pro jednotlivá povodí byla interpolací Thiessenovými polygony spočítána průměrná srážka na povodí, ta byla následně korigována na základě vrstvy průměrných srážek (stejné období, rozlišení 1 km × 1 km) tak, aby průměr srážek pro povodí byl stejný. Podoba byla korigována i teplota – průměrná teplota na povodí z gridované vrstvy byla opravena na základě rozdílu v nadmořské výšce odvozené z gridované vrstvy a z digitálního modelu terénu, přičemž byl uvažován gradient teploty 0.65 °C/100 m. Gridovaná datová sada (v denním kroku) byla využita i pro tvorbu scénářů změny klimatu pomocí korekce systematických chyb (viz kapitola 4.1) i pokročilé přírůstkové metody (viz kapitola 4.2).
1.2 Regionální klimatické modely z projektu ENSEMBLES
Projekt ENSEMBLES (Hewitt a Griggs 2004) byl významným projektem financovaným z programu EU FP7, na němž participovaly desítky zejména evropských institucí. V rámci projektu byla provedena řada simulací globálních a regionálních klimatických modelů, většinou pro Evropu, ale i pro západní Afriku. Simulace regionálních klimatických modelů jsou dostupné jednak jako čtyřicetileté časové řezy řízené reanalýzou ERA-40 a tzv. transientní simulace řízené globálními klimatickými modely pro období 1950–2050 nebo i 1950–2100. Data regionálních klimatických modelů jsou ke stažení na http://ensemblesrt3.dmi.dk/.
V této práci byly použity simulace řízené emisním scénářem SRES A1B (jiné emisní scénáře se v ENSEMBLES datech vyskytují velmi sporadicky) pokrývající období 1961–2099 s prostorovým rozlišením 25 km × 25 km. Uvažováno bylo 15 RCM simulací řízených 4 GCM modely (viz Tab. 1.1). Nejvíce simulací bylo provedeno s modelem RCA (4). Zvláštní postavení v tomto souboru modelů mají HadRM simulace, jelikož se jedná o tři členy tzv. perturbed physics ensemblu – tj. souboru, který vznikl systematickou obměnou parametrů modelu HadRM. Model HadRM_Q0 je model se standardním nastavením, HadRM_Q3 (HadRM_Q16) je model s nejnižší (nejvyšší) odezvou na radiační působení (viz Collins et al. 2006).
Tab. 1.1. Použité simulace regionálních klimatických modelů
| Model | Akronym | Zdroj |
|---|---|---|
| řízené modelem ECHAM5 | ||
| RACMO | RACMO_EH5 | Královský nizozemský meteorologický institut (KNMI) |
| REMO | REMO_EH5 | Max-Planck Institut (MPI), Německo |
| RCA | RCA_EH5 | Švédský hydrometeorologický institut (SMHI) |
| RegCM | RegCM_EH5 | Mezinárodní centrum pro teoretickou fyziku (ICTP), Itálie |
| HIRHAM | HIR_EH5 | Dánský meteorologický institut (DMI) |
| řízené modelem HadCM3Q0, HadCM3Q3, HadCM3Q16 | ||
| HadRM | HadRM_Q0 | Hadley Centre, UK |
| CLM | CLM_Q0 | Federální švýcarský technologický institut (ETHZ) |
| HadRM | HadRM_Q3 | Hadley Centre, UK |
| RCA | RCA_Q3 | Švédský hydrometeorologický institut (SMHI) |
| HadRM | HadRM_Q16 | Hadley Centre, UK |
| RCA | RCA_Q16 | Komunitní sdružení pro klimatickou změnu (C4I), Irsko |
| řízené modelem ARPEGE | ||
| HIRHAM | HIR_ARP | Dánský meteorologický institut (DMI) |
| CNRM-RM | CNRM_ARP | Národní centrum pro meteorologický výzkum (CNRM), Francie |
| ALADIN-CLIMATE/CZ* | ALA_ARP | Český hydrometeorologický ústav (ČHMÚ), Česká republika |
| řízené modelem BCM | ||
| RCA | RCA_BCM | Švédský hydrometeorologický institut (SMHI) |
*) tato simulace vznikla v rámci řešení projektu VaV – Zpřesnění dosavadních odhadů dopadů klimatické změny v sektorech vodního hospodářství, zemědělství a lesnictví a návrhy adaptačních opatření
1.3 Globální klimatické modely z projektu CMIP5
Coupled Model Intercomparison Project (CMIP), v současnosti v páté fázi (tj. CMIP5), byl zahájen roku 2008 a je cílen na vytvoření rámce pro koordinaci experimentů s klimatickým modelováním, zejména se zaměřením na Pátou hodnotící zprávu IPCC (Stocker et al. 2013). Deklarovaným cílem projektu je vytvoření multi-modelového kontextu sloužícího k (1) hodnocení mechanismů zodpovědných za rozdíly v simulacích zpětných vazeb spojených zejména s cyklem uhlíku a tvorbou oblačnosti, (2) prověření schopnosti modelů predikovat klima v měřítku desetiletí a (3) nalezení důvodů odlišností projekcí stejně řízených modelů.
CMIP5 modely využívají (mimo jiné) scénáře koncentrací RCP. Celý soubor modelů je unikátní svou velikostí – v době shromažďování dat pro tuto studii byla k dispozici data z 30 GCM z 18 institucí, celkem 191 simulací (viz Tab. 1.2). Jednotlivé RCP scénáře nejsou zastoupeny rovnoměrně – pro RCP8.5 je k dispozici 63 simulací, pro RCP6.0 pouze 29. Pro některé GCM je k dispozici několik simulací pro daný RCP scénář (nejvíc, 10 pro CSIRO-Mk3-6-0), nicméně většina modelů má jen jednou simulaci pro daný RCP scénář. Navíc ne všechny modely disponují simulacemi pro všechny RCP scénáře.
K dispozici byla denní GCM data interpolovaná na společném 1.25° × 2° gridu pro období 1961–1995, 2021–2050 a 2071–2100.
Tab. 1.2. Počet dostupných simulací pro všechny použité kombinace GCM a RCP (MODEL: identifikátor globálního modelu, ACM: identifikátor atmosférického modelu)
| MODEL | ACM | RCP | \(\mathbf{\sum}\) | MODEL | ACM | RCP | \(\mathbf{\sum}\) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.6 | 4.5 | 6.0 | 8.5 | 2.6 | 4.5 | 6 | 8.8 | ||||||
| CNRM-CM5 | ARPEGE | 1 | 1 | - | 1 | 3 | GFLD-CM3 | GFLD | 1 | - | 1 | 1 | 3 |
| EC-EARTH | - | - | - | 8 | 8 | GFDL-ESM2G | 1 | 1 | 1 | 1 | 4 | ||
| bcc-csm1-1 | BCC | 1 | 1 | 1 | 1 | 4 | GFDL-ESM2M | 1 | 1 | 1 | 1 | 4 | |
| bcc-csm1-1-m | 1 | 1 | 1 | 1 | 4 | GISS-E2-R | GISS | - | 1 | - | - | 1 | |
| MRI-CGCM3 | MRI | 1 | 1 | 1 | 1 | 4 | ACCESS1-3 | GA | - | 1 | - | 1 | 2 |
| BNU-ESM | CAM | 1 | 1 | - | 1 | 3 | ACCESS1-4 | HadGEM | - | 1 | - | 1 | 2 |
| CCSM4 | 3 | 3 | 3 | 3 | 12 | HadGEM-CC | - | 1 | - | 3 | 4 | ||
| NorESM1-M | 1 | 1 | 1 | 1 | 4 | HadGEM2-ES | 4 | 4 | 4 | 4 | 16 | ||
| CanESM2 | CanCM | 5 | 5 | - | 5 | 15 | inmcm4 | INCM | - | 1 | - | 1 | 2 |
| CSIRO-Mk3-6-0 | CSIRO | 10 | 10 | 10 | 10 | 40 | IPSL-CM5A-LR | IPSL | 4 | 4 | 1 | 4 | 13 |
| CMCC-CESM | ECHAM | - | - | - | 1 | 1 | IPSL-CM5A-MR | 1 | 1 | 1 | 1 | 4 | |
| CMCC-CM | - | 1 | - | 1 | 2 | IPSL-CM5B-LR | IPSL-B | - | 1 | - | 1 | 2 | |
| CMCC-CMS | - | 1 | - | 1 | 2 | MIROC5 | MIROC | 3 | 3 | 1 | 3 | 10 | |
| MPI-ESM-LR | 3 | 3 | - | 3 | 9 | MIROC-ESM | 1 | 1 | 1 | 1 | 4 | ||
| MPI-ESM-MR | 1 | 3 | - | 1 | 5 | MIROC-ESM-CHEM | 1 | 1 | 1 | 1 | 4 | ||
| \(\mathbf{\sum}\) | 45 | 54 | 29 | 63 | 191 |
2 Hydrologický model Bilan a jeho kalibrace
Hydrologický model Bilan (Horáček et al. 2009) schematizuje povodí na soustavu nádrží ve třech vertikálních úrovních – povrch, půdní zóna a zóna podzemní vody. Velikost toků mezi jednotlivými nádržemi je určována algoritmy modelu, které jsou řízeny v měsíční verzi osmi a v denní verzi šesti volnými parametry (viz Tab.2.1). Vstupem do modelu jsou pozorované časové řady srážek a teploty vzduchu. Potenciální evapotranspirace je vypočítána pomocí jednoduché metody (Oudin et al. 2010; Beran et al. 2011) vycházející z teploty vzduchu a množství slunečního záření dopadajícího na horní vrstvu atmosféry (ovlivněno zeměpisnou šířkou a dnem v roce), popřípadě na základě metodiky (Gidrometeoizdat, 1976) vycházející z empirických vztahů (odvozených pro různé vegetační zóny) mezi potenciální evapotranspirací a sytostním doplňkem vypočteným z teploty a relativní vlhkosti vzduchu. Bilance na povrchu půdy je určena vstupními srážkovými úhrny a územním výparem stanoveným na základě potenciální evapotranspirace a množství dostupné vody. V zimním období a při tání sněhu vstupuje do bilance na povrchu zásoba vody ve sněhu. Z povrchu voda infiltruje do půdní zóny, kde plní nádrž s kapacitou, která je jedním z kalibrovaných parametrů. Při překročení této kapacity voda přetéká a následně je dělena do dvou lineárních nádrží. Odtoky z nich představují pomalou (základní odtok) a rychlou (přímý odtok) odezvu povodí, celkový odtok je pak dán jejich součtem (Horáček et al. 2009).
Tab. 2.1. Parametry modelu Bilan
| Parameter | Význam |
|---|---|
| Spa | maximální zásoba vody v půdě |
| Alfa | koeficient nádrže přímého odtoku (denní krok) / odtoku z půdní zásoby a srážky (měsíční krok) |
| Grd | koeficient nádrže základního odtoku |
| Dgm | míra tání sněhu v závislosti na teplotě v režimu tání |
| Dgw | míra tání sněhu v zimním režimu |
| Wic, Mec, Soc | poměr perkolované vody nepodílející se na doplnění zásoby podzemní vody |
Za účelem kalibrace modelu Bilan byly shromážděny dostupné měsíční časové řady pozorovaných srážek a teploty pro plochy 130 zvolených povodí pro období 1961–2010. Dále byly odvozené odtokové řady pro uzávěrové profily jednotlivých povodí. Pro 68 povodí jsou k dispozici časové řady průtoků pro celé období, 98 povodí má řadu aspoň 40 let, 109 povodí aspoň 30 let, 118 povodí aspoň 20 let a 124 povodí aspoň 10 let. Pro 4 povodí (DBCN 153200, 169000, 205000, 480500) nebyla k dispozici žádná použitelná data. Jelikož se nejedná ve všech případech o uzavřená povodí, ale spíše úseky vodních toků, je výpočet odtoku často problematický – v důsledku nepřesností a chyb měření vychází při odčítání průtoků pro jednotlivá dílčí povodí v některých měsících záporné průtoky. Pro 88 povodí se v řadách nevyskytovaly záporné průtoky, pro 115 povodí byl podíl záporných průtoků do 10 % (Obr. 2.1). Počet let s použitelnými daty a poměr záporných průtoků v řadách je zobrazen v mapě na Obr. 2.2.
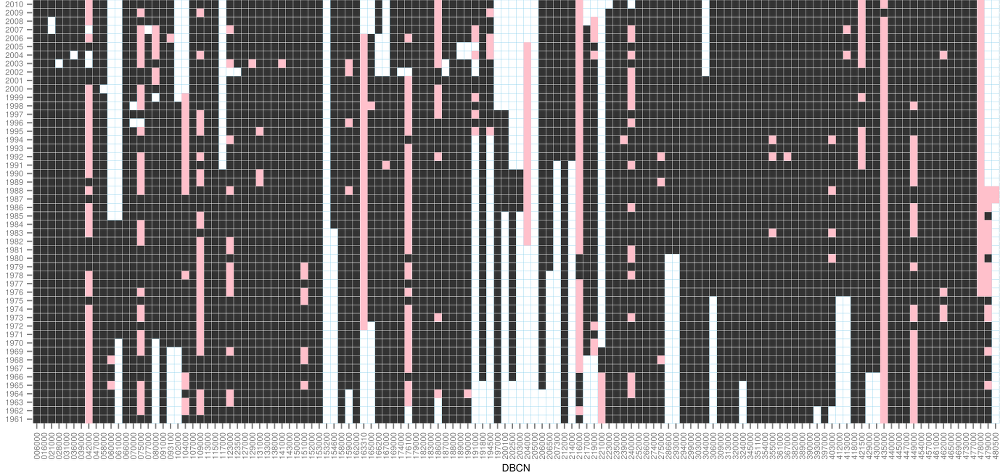
Obr. 2.1 Přehled dat. Černě jsou vyznačeny roky s použitelnými daty, roky se zápornými průtoky jsou vyznačeny růžově, bíle jsou vyznačeny roky bez dat.
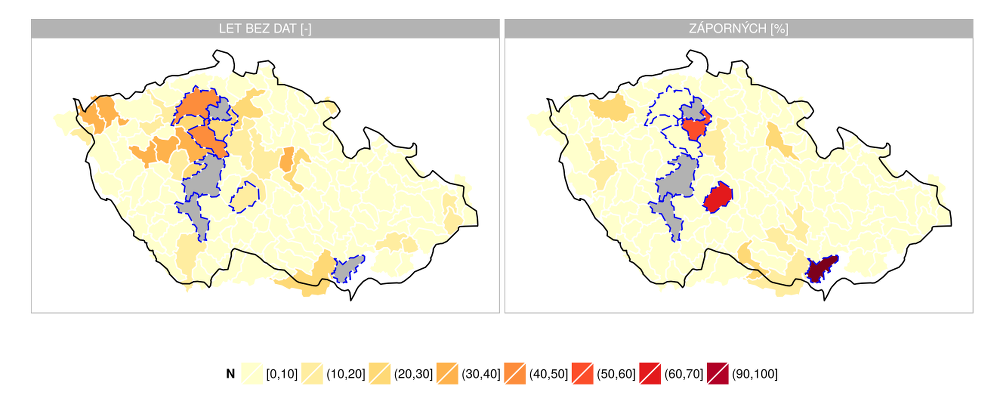
Obr. 2.2 Počet let bez dat v období 1961–2010 (vlevo) a poměr záporných průtoků (vpravo). Šedě jsou vyznačena povodí, pro něž nebyla k dispozici žádná využitelná data. Modře jsou ohraničena povodí, pro která je řada využitelných dat kratší než 10 let nebo poměr záporných dat vyšší než 25 %.
Příčinou výskytu záporných hodnot v jednotlivých případech a systematických chyb při odvození odtoku z mezipovodí obecně může částečně být doba postupu mezi jednotlivými profily a případné užívání vod. Velkou měrou se však na velikosti systematické chyby může podílet nepřesnost měření průtoku v odečítaných profilech. Podrobný rozbor těchto chyb za zjednodušených předpokladů předkládá (Kašpárek 1989). Nechť \(Q_d\) je průtok v dolním profilu a průtok v horním profilu je \(K\)násobkem průtoku v dolním profilu, tj. \(Q_h = K Q_d\) a relativní chyba měření \(r\) je v obou profilech stejná. Jak se v konkrétním případě sčítají, nebo vzájemně částečně eliminují dílčí chyby \(r Q_h\) a \(r Q_d\) není jisté. Celkovou chybu \(e_r\) je možno odvodit pomocí součtu kvadratických chyb, tj. \(e_r = \sqrt{(r Q_h)^2+(r Q_d)^2} = r Q_d \sqrt{1 + K^2}\), nicméně může nastat i nepříznivější případ, kdy se chyby sečtou, tj. \(e^*_r = r (Q_h + Q_d) = r Q_d (1 + K)\). Po úpravě těchto výrazů dostáváme pro relativní chybu odtoku \(e_r\) vztah
\[e_r = \frac{r \sqrt{1+ K^2}}{1-K},\](2.1)
respektive pro nepříznivý případ
\[e_r^* = \frac{r (1+K)}{1-K}.\](2.2)
Koeficient \(K\) je možné odvodit z průtokových řad, nicméně ty jsou již ovlivněny analyzovanou systematickou chybou. Druhou možností je využít hydrologické analogie, tj. odvodit koeficient \(K\) na základě poměru ploch dílčích povodí. Takto odvozený koeficient \(K\) i kategorizace povodí do tří tříd dle velikosti \(e_r\) ukazuje Obr. 2.3. Je evidentní, že chyba odhadu odtoku z mezipovodí může být v některých případech enormní. Jde zejména o případy velkých povodí, pro které je poměr plochy mezipovodí (ta je řádově srovnatelná pro 130 vybraných povodí) k ploše zbytku povodí malý.
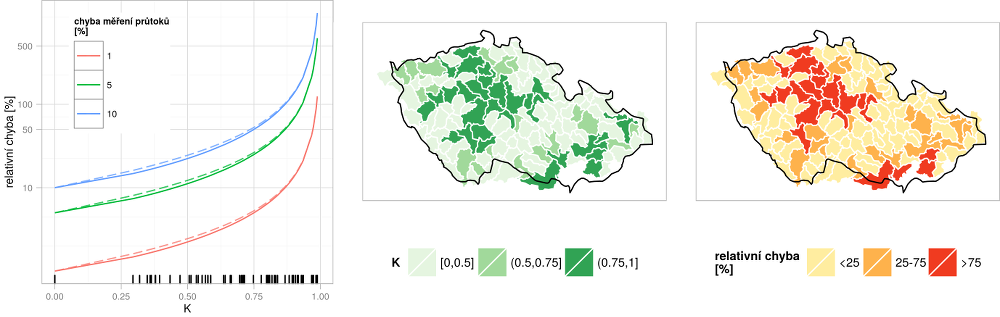
Obr. 2.3 Průběh relativní chyby odhadu odtoku z mezipovodí pro různé chyby měření – \(e_r\) plnou čárou, \(e_r^*\) čárkovaně (vlevo), koeficient \(K\) z rovnic – odvozený z rozdílu ploch (uprostřed) a relativní chyba odhadu odtoku z mezipovodí pro chybu měření 10 % (vpravo).
Kalibrace probíhala pomocí prostředků modelu Bilan, tj. parametry byly optimalizovány pomocí gradientní metody nebo diferenciální evoluce (Máca et al. 2013). Obě metody umožňují volbu optimalizačního kriteria z kritérií standardně využívaných pro kalibraci hydrologických modelů (Nash-Sutcliffe – NSE, log NSE, střední kvadratická chyba – RMSE, střední absolutní chyba – MAE, střední relativní chyba – MAPE). Kvůli výskytu záporných hodnot byl optimalizační algoritmus modelu Bilan upraven tak, že umožňuje jednotlivým pozorováním přiřadit váhy, které se použijí pro výpočet optimalizačního kritéria při kalibraci. Přiřazením nulových nebo záporných vah je tak možné zcela eliminovat vliv záporných hodnot na hodnotu optimalizačního kritéria, respektive výsledných parametrů. Pro řadu povodí byla využita i možnost kalibrace se zohledněním odhadu základního odtoku. Odhad základního odtoku metodou klouzavých minim poskytl ČHMÚ.
Pro každé povodí byly testovány různé optimalizační metody, kriteriální funkce, kalibrační období atp. Pro povodí bez kvalitních dat byly použity sady parametrů přenesené z blízkých povodí. V řadě případů probíhala (vzhledem k povaze dat) kalibrace spíš expertním odhadem než na základě striktní minimalizace/maximalizace optimalizačního kritéria. Výsledky kalibrace vyjádřené hodnotami kriteriálních funkcí nejsou na první pohled zcela uspokojivé. Nicméně zohledníme-li kategorizaci povodí dle chyby odhadu odtoku z mezipovodí (viz Obr. 2.4) zjistíme, že povodí, která jsou zatížena menší chybou odhadu odtoku, vykazují zároveň přijatelné hodnoty kriteriálních funkcí. Naopak pro povodí s nespolehlivými daty indikují kritéria rozpory mezi odhadnutými a simulovanými hodnotami. Neuspokojivé hodnoty kriteriálních funkcí lze tak přinejmenším částečně připsat chybám vyčíslení průtoků.
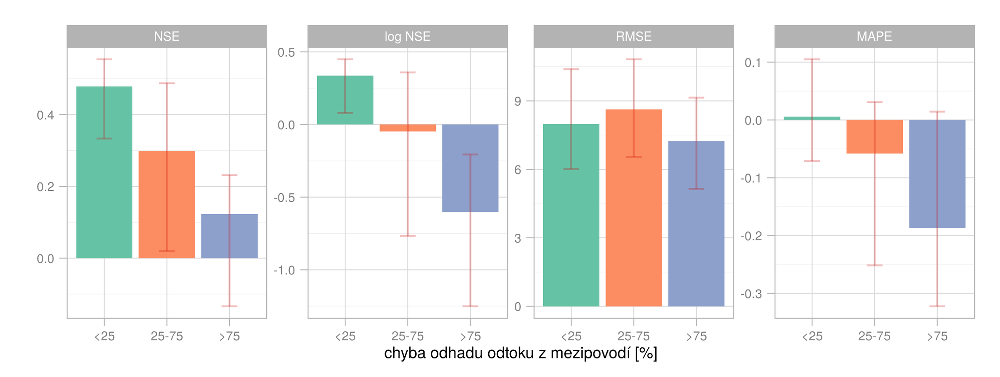
Obr. 2.4 Sloupcový graf udává mediány kriteriálních funkcí pro různé kategorie spolehlivosti odhadů odtoku z mezipovodí. Čáry udávají mezikvartilové rozpětí pro povodí spadající do dané kategorie.
Vzhledem k obtížné kalibraci jsme se zaměřili na validaci simulovaných odtoků pomocí empirických vztahů a na analýzu výsledných parametrů. V prvním kroku byly revidovány výsledné sady parametrů pro povodí, kde některý z parametrů nabýval neobvyklých hodnot (zpravidla hodnot blízkých jedné z mezí intervalů pro kalibraci jednotlivých parametrů).
Následně bylo pro jednotlivá povodí vyhodnoceno, zdali je simulovaný celkový a základní odtok konzistentní s empirickými odhady, které udává např. Kašpárek et al. (2012). Uvažované empirické vztahy byly odhadnuty z několika datových sad zahrnujících desítky povodí. Bylo by samozřejmě možné zahrnout tyto vztahy přímo do optimalizace modelu Bilan, nicméně to by vedlo jen k umělému potvrzování těchto vztahů.
Pro povodí s roční průměrnou srážkou (\(P_a\)) vyšší než 400 mm lze průměrnou roční odtokovou výšku (\(R_a\)) stanovit dle
\[R_a = 0.000571P^2_a + 0.132P_a - 170.2\](2.3)
alternativu udává Kašpárek et al. (2000) v podobě
\[R_a = P_a + 0.519P^{1.236}_a - 2.967P_a - 98.1\](2.4)
Z fyzikálního hlediska je nevýhodou výše zmíněných rovnic, že zcela ignorují vliv teploty na výpar, a tedy i velikost odtoku. Kašpárek et al. (2012) uvádí empiricky zjištěné vztahy pro odhad průměrné roční potenciální evapotranspirace (\(PE_a\)) na základě průměrné roční teploty (\(T_a\))
\[PE_a = 37.97 T_a + 289.4\](2.5)
i vztah pro poměr skutečně evapotranspirované vody (\(E_a\)) k potenciální evapotranspiraci
\[{\frac{E_a}{PE_a}} = 0.98 (1 - 0.22 ^ {\frac{P_a}{PE_a}}).\](2.6)
S využitím hydrologické bilance \(R_a = P_a - E_a\) lze z těchto vztahů vyjádřit \(R_a\) jako
\[R_a = P_a - 0.98 PE_a (1 - 0.22 ^ {\frac{P_a}{PE_a}}).\](2.7)
Empirický vztah pro průměrný základní odtok (\(q_z\) [l/s/km²]) odvodil Krásný et al. (1982) pro povodí bez významných přírodních zdrojů:
\[q_z = 0.00001924 P_a^2 - 0.01251257 P_a + 2.06052230.\](2.8)
Beran et al. (2014) odvodil na základě řešení projektu Rebilance zásob podzemních vod vztah pro průměrný roční základní odtok (\(BF\) [mm/rok])
\[BF = 0.0004 P_a^2 - 0.0276 P_a - 56.978.\](2.9)
Podobně jako v rovnicích 2.3 a 2.4, není zde uvažován vliv teploty.
Porovnání modelovaného celkového a základního odtoku s empirickými odhady ukazuje Obr. 2.5. Celkový modelovaný odtok dobře koresponduje s empirickými odhady. Základní odtok je v modelu Bilan oproti empirickým odhadům o něco vychýlen (cca −15 % při použití vzorce dle Krásný et al. (1982), respektive cca +13 % při použití vzorce dle Beran et al. (2014)). V každém případě lze vzhledem k nepřesnostem měření a chybám odhadu základního odtoku považovat simulované hodnoty za přijatelné.
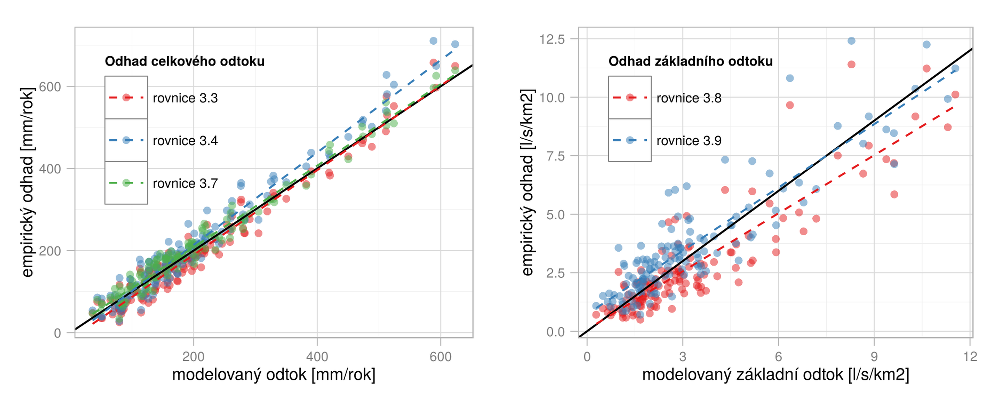
Obr. 2.5 Porovnání modelovaného celkového (vlevo) a základního (vpravo) odtoku s empirickými vztahy. Čárkovaná čára ukazuje proložení lineárním modelem.
Nakalibrované parametry byly posléze použity pro několik typů simulací:
simulace pro pozorované podmínky na základě homogenní gridované datové sady srážek a teploty pro období 1961–2010 (viz kapitola 3).
simulace pro scénáře změny klimatu dle korigovaných simulací regionálních klimatických modelů z projektu ENSEMBLES (viz kapitola 4.1)
simulace pro scénáře změny klimatu dle korigovaných simulací regionálních klimatických modelů z projektu CMIP5 (viz kapitola 4.2)
Z globálního pohledu jsou vystiženy důležité rysy hydrologického režimu v ČR. V jednotlivých případech nemusí být výsledné parametry a dlouhodobé průměry simulovaných veličin optimální. Na odstranění těchto nedostatků se dále pracuje. Proto i dále prezentované výsledky je vhodné interpretovat spíše regionálně v rámci ČR či oblastí povodí.
3 Probíhající změny
Změnu klimatu ovlivňující hydrologický režim lze v České republice pozorovat již řadu let. Nejmarkantněji jsou změny patrné na teplotách vzduchu. Interpolujeme-li teploty vzduchu na plochy povodí, zjistíme, že průměrná roční teplota vzrostla mezi obdobími 1961–1990 a 1980–2010 o 0.6 °C, v létě až o 0.9 °C, naopak na podzim pouze o 0.2 °C (viz Obr. 3.1). Změny teploty jsou prostorově poměrně homogenní – rozdíl v růstu teploty mezi povodími je pro jednotlivá roční období většinou do 0.5 °C, zatímco rozdíl ve změnách pro různá roční období je pro jednotlivá povodí až 1 °C.
Teplota je zásadní faktor ovlivňující hydrologickou bilanci zejména z toho důvodu, že s rostoucí teplotou roste množství vody, které se může vypařit, případně být transpirováno rostlinami, tj. s rostoucí teplotou roste potenciální evapotranspirace. Podobně jako v případě teploty jsou změny potenciální evapotranspirace prostorově homogenní a v jednotlivých ročních obdobích dosahují v průměru 5 %, nejvíce pak v zimním období (10 %), což je způsobeno vyšším počtem dní s teplotami umožňující výpar a nejméně na podzim (1 % – srov. změny teploty). Po přepočtu na výšku vodního sloupce odpovídají tyto změny v součtu za celý rok přibližně 25 mm, přičemž nejvíce (13 mm) připadá na léto a nejméně (1 mm) na podzim. Přes velký relativní růst potenciální evapotranspirace v zimě je absolutní změna v tomto období rovněž velmi malá (1.5 mm).
Ve skutečnosti jsou však změny evapotranspirace menší, což je způsobeno tím, že není k dispozici dostatek vody pro výpar a transpiraci rostlin. Reálná evapotranspirace (Obr. 3.2 ) tak roste v průměru o 3 % (tj. ročně o 11 mm) a pouze v zimním období se tento růst zhruba rovná potenciální evapotranspiraci. V ostatních ročních obdobích se změny pohybují v řádu jednotek procent, což na jaře a v létě odpovídá cca 5 mm.
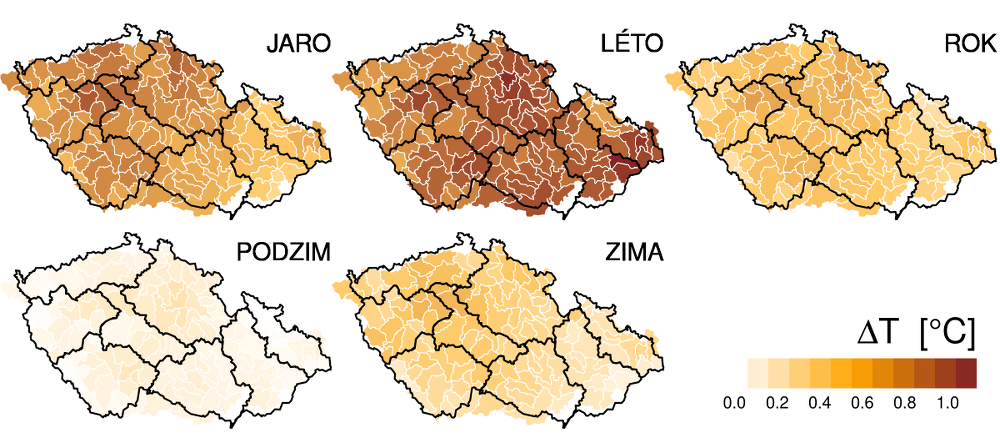
Obr. 3.1 Změny teploty mezi obdobími 1961–1990 a 1980–2010 pro různá roční období.
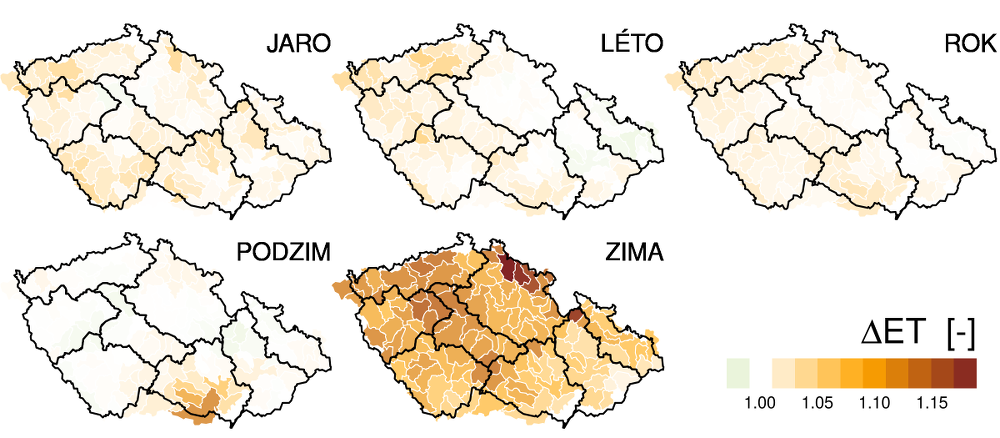
Obr. 3.2 Změny reálné evapotranspirace (odhad pomocí hydrologického modelu) mezi obdobími 1961–1990 a 1980–2010 pro různá roční období.
Pro hydrologický režim je příznivé, že pozorovaný růst teploty a potenciální i skutečné evapotranspirace je doprovázen mírným růstem srážek (Obr. 3.3). Roční průměrný srážkový úhrn vzrostl mezi obdobími 1961–1990 a 1981–2010 o 3 % (23 mm), na jaře stagnoval a v ostatních ročních obdobích rostl přibližně o 5 % (cca 7 mm). Změny srážek jsou na rozdíl od změn teploty a evapotranspirace značně prostorově proměnlivé. Za zmínku stojí zejména oblast středních Čech, kde došlo k poklesu jarních srážkových úhrnů (až o 10 %). Tento pokles se podílí i na stagnaci, jinde rostoucích, ročních srážkových úhrnů v této oblasti. Částečným vysvětlením pro tuto heterogenitu mohou být dlouhodobé změny atmosferické cirkulace. Rozdíly ve změnách srážek mezi jednotlivými povodími jsou pro všechna roční období do 20 %. To je zhruba stejně jako maximální rozdíly ve změnách srážek mezi ročními obdobími pro jednotlivá povodí.
V roční bilanci dochází na velké části našeho území k účinné kompenzaci růstu potenciální evapotranspirace zvýšenými srážkami. V průměru tak dochází k mírnému zvýšení ročních odtokových výšek (cca 4 %, 10 mm), viz Obr. 3.4. Toto zvýšení, ale není plošné – zhruba na čtvrtině vyhodnocovaných povodí dochází k poklesu odtoku (v létě téměř na polovině, na podzim pouze na desetině). To se týká zejména oblasti středu Čech vykazující v některých částech dlouhodobě pasivní hydrologickou bilanci. Právě v těchto oblastech se vyskytují povodí, ve kterých lze již v současnosti pozorovat negativní dopady změny (či variability) klimatu v podobě nedostatku vodních zdrojů v některých letech. Příkladem mohou být povodí Rakovnického potoka, Srpiny, Blšanky, pro která se v minulých letech řešily návrhy adaptačních opatření zmírňující tyto dopady. V současnosti se jedná zejména o povodí přirozeně chudá na srážky, nicméně v budoucnu (naplní-li se projekce klimatických modelů) můžeme očekávat podobné problémy i v jiných oblastech České republiky.
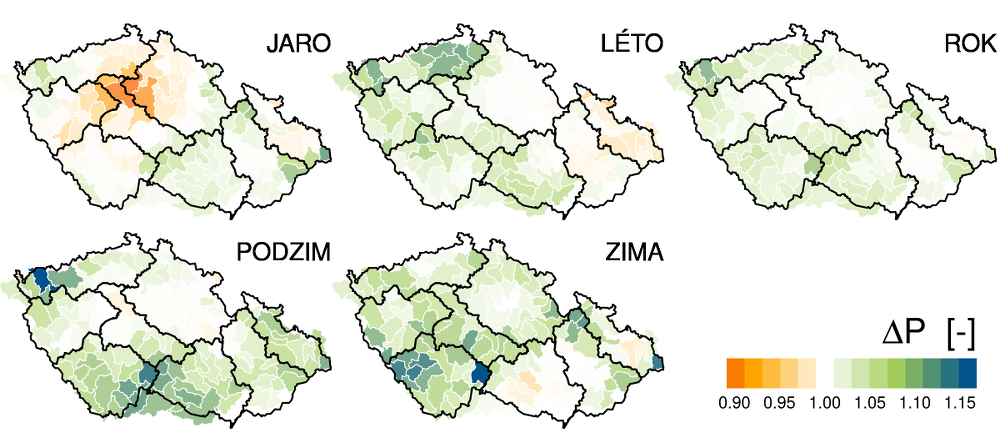
Obr. 3.3 Změny srážek mezi obdobími 1961–1990 a 1980–2010 pro různá roční období.
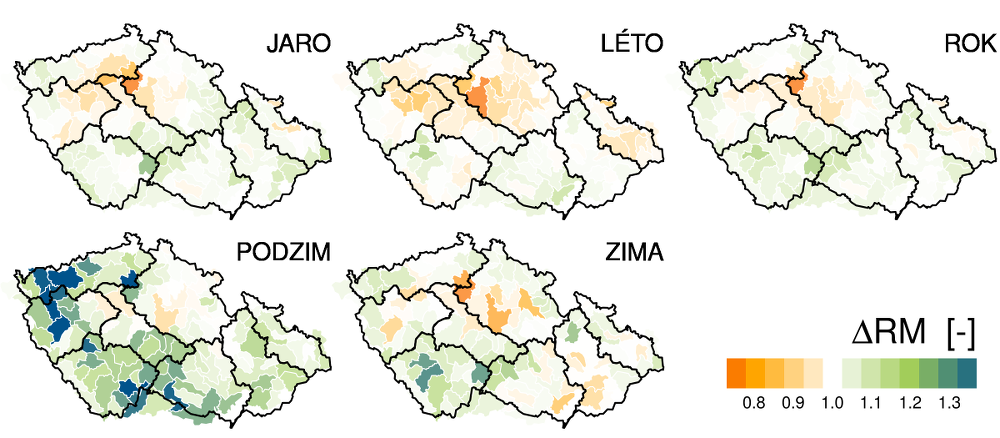
Obr.3.4 Změny odtoku (odhad hydrologickým modelem) mezi obdobími 1961–1990 a 1980–2010 pro různá roční období.
4 Scénáře změny klimatu
Pro posouzení možných změn hydrologického režimu na povodích v ČR byly kromě pozorovaných změn uvažovány dvě sady scénářů klimatické změny založené na výstupech projektu ENSEMBLES a CMIP5. Zároveň byly z vybrány tři reprezentativní simulace (z ENSEMBLES dat) pro posouzení průběhu možných realizací budoucího hydrologického režimu. Tyto sady scénářů popisují následující kapitoly.
4.1 Korekce systematických chyb – ENSEMBLES data
Simulace regionálních klimatických modelů z Tab.1.1 byly s použitím gridovaných pozorování teploty a srážek v denním kroku opraveny o systematické chyby pomocí tzv. kvantilové metody (viz např. Gudmundsson et al. 2012). Tato (široce užívaná) metoda byla zvolena mimo jiné proto, že simulace modelu ALADIN-CLIMATE/CZ byla dostupná již zkorigovaná touto metodou. Tato metoda spočívá v odvození transferové funkce, jež zaručuje, že hodnoty transformované řady odpovídají stejným kvantilům jako příslušné hodnoty řady původní. Období, vzhledem ke kterému byly simulace zkorigovány, bylo zvoleno stejné jako v případě ALADIN-CLIMATE/CZ, tj. 1961–1990.
Formálně lze korekci rozdělení pravděpodobnosti simulované veličiny \(P_m\) (např. srážek simulovaných klimatickým modelem) pomocí rozdělení pozorované veličiny \(P_O\) (např. pozorované srážky) zapsat jako transformaci
\[P_O = h(P_m)\](4.1)
Transformované rozdělení \(h(P_m)\) je pak stejné jako rozdělení pozorované veličiny. Transformace \(h\) je odvozena pomocí tzv. probability integral transformation – tj. je využito toho, že distribuční funkce libovolné spojité veličiny má rovnoměrné rozdělení. Transformace má pak podobu
\[P_O = F_O^{-1}[F_m(P_m)]\](4.2)
kde \(F_m\) je (empirická) distribuční funkce získaná ze simulovaných dat pro kontrolní klima a \(F_O^{-1}\) je empirická kvantilová funkce odvozená z pozorovaných řad. V praktických aplikacích je často součástí této metody i statistický model rozdělení dané veličiny (a z dat se odhadují jen parametry tohoto rozdělení). V této práci nicméně zůstáváme u empirické distribuční a kvantilové funkce. Zjednodušeně se dá postup popsat tak, že nejprve je zjištěna pravděpodobnost dosažení simulované srážky a následně je za ni dosazena hodnota z pozorovaných dat se stejnou pravděpodobností. Pro budoucí klima je zjišťováno, jakou pravděpodobnost mají hodnoty veličin na základě distribuční funkce pro kontrolní klima (\(F_m\)), následně je použita distribuční funkce \(F_O^{-1}\). Metoda se zpravidla aplikuje po jednotlivých měsících.
S aplikací metody je spojeno několik úskalí. V případě srážek jde zejména o to, že metoda nedokáže korigovat problémy s počtem dní se srážkami, respektive v případě, že je počet dní se srážkami malý, nedokáže dny přidávat. Pro většinu klimatických modelů je nicméně typický spíše opačný případ, tj. že počet dní se srážkami je příliš vysoký. Dalším problémem, který je spojený jak s korekcí srážek, tak i teploty, je, že není jasné, jak pro budoucí klima korigovat hodnoty, které jsou vyšší (nebo nižší) než v případě simulace pro kontrolní klima. Zde se zpravidla uvažuje lineární extrapolace nejvyšších hodnot.
Obr. 4.1 a Obr.4.2 ukazují původní chybu v odhadu srážek a teploty a chybu v korigovaných datech. Letní srážky jsou obecně simulovány lépe (systematická chyba většinou v rozmezí −25 %–25 %) než srážky po zbytek roku (většinou nadhodnoceny o 30 %–80 %). Průměrná chyba se pohybuje okolo 30 %. Je zřejmé, že korekce dokáže systematické chyby u jednotlivých modelů obecně dobře odstranit. Výjimkou jsou simulace, které výrazně podhodnocují letní srážky a vykazují příliš vysoký podíl dní beze srážek (zejména HIR_ARP). Provedeme-li validaci korekčních vztahů na období 1981–2010, zjistíme, že systematická chyba narůstá, nicméně stále je v porovnání s původní simulací relativně malá (většinou ±10 %).
Letní teplotu většina RCM nadhodnocuje (až 5 °C – opět HIR_ARP), pro ostatní roční období se systematická chyba pohybuje pro většinu RCM v rozmezí ±1.5 °C. Kvantilová metoda dokáže tyto systematické chyby spolehlivě odstranit (v období, na které je použita), nicméně při validaci na období 1981–2010 se objevuje pro letní teplotu systematické podhodnocení o cca 1 °C, což signalizuje, že systematická chyba není stacionární, respektive může být do značné míry ovlivněna dlouhodobou variabilitou klimatu. Nestacionaritu systematických chyb zmiňuje např. Reifen a Toumi (2009) nebo Ehret et al. (2012), nicméně přesto je korekce systematických chyb široce využívanou metodou.
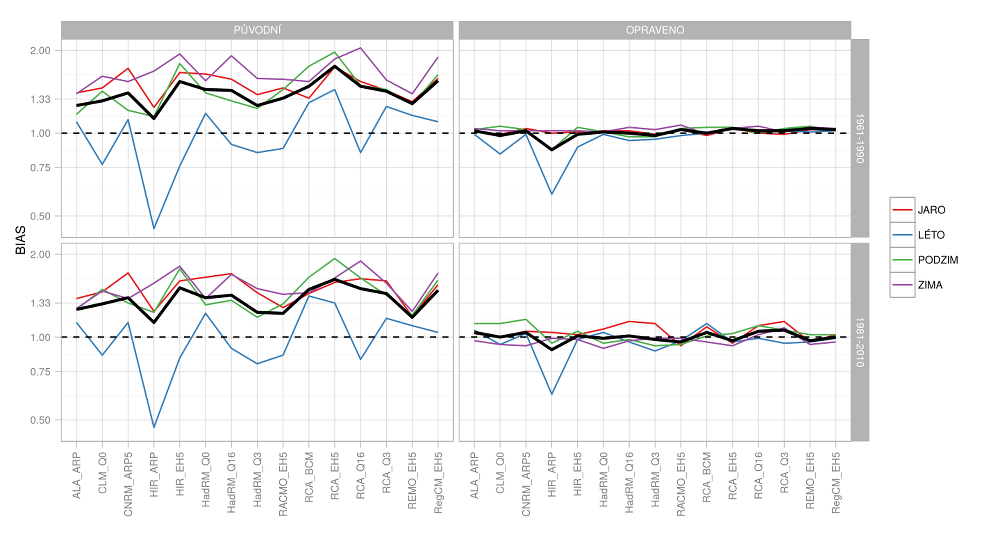
Obr.4.1 Systematická chyba (průměr pro ČR) v průměrné sezónní (barevné čáry) a roční (tlustá čára) srážce pro původní a korigovaná data v porovnání s různými pozorovanými obdobími.
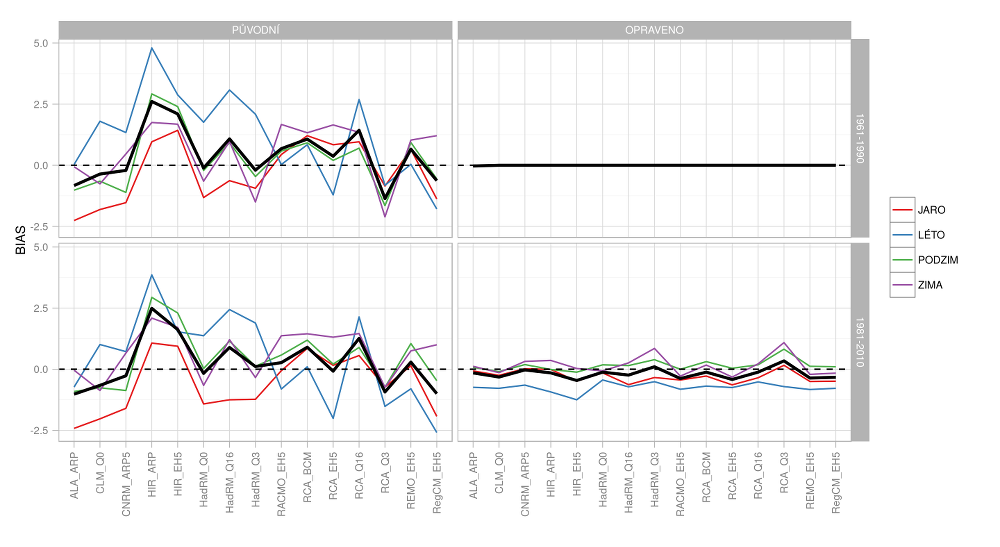
Obr.4.2 Systematická chyba (průměr pro ČR) v průměrné sezónní (barevné čáry) a roční (tlustá čára) teplotě pro původní a korigovaná data v porovnání s různými pozorovanými obdobími.
Systematická chyba v simulaci maximálního sezónního srážkového úhrnu (tj. úhrnu srážek za 3 měsíce) je srovnatelná s chybou průměrného úhrnu (Obr. 4.3). Je evidentní, že kvantilová metoda aplikovaná v denním kroku nedokáže opravit systematické chyby v maximálních sezónních úhrnech. Důvodem je, že metoda nezohledňuje perzistenci v časové řadě – tj. přesto, že rozdělení denních hodnot korigované simulace víceméně přesně odpovídá pozorování, pro rozdělení měsíčních, sezónních a ročních úhrnů (a průměry teploty – viz Obr. 4.4 ) to neplatí. Ze statistik korigovaných řad na Obr. 4.3 (vpravo nahoře) je evidentní, že klimatické modely podhodnocují výskyt delších období se srážkami, zejména v zimě. Podobně na Obr. 4.4 je patrná přílišná koncentrace dnů s nízkými teplotami v letním období a dnů s vyššími teplotami v zimním období pro cca polovinu modelů.
Alternativou, která je nicméně nad rámec této práce, je kaskádová korekce (nebo přírůstková metoda), kterou popisuje např. Haerter et al. (2011). Podstatou této metody je postupná korekce od dlouhých časových měřítek (např. sezónních) ke krátkým (např. denním). Korigovány jsou pak odchylky od průměrů vyšší časové agregace.
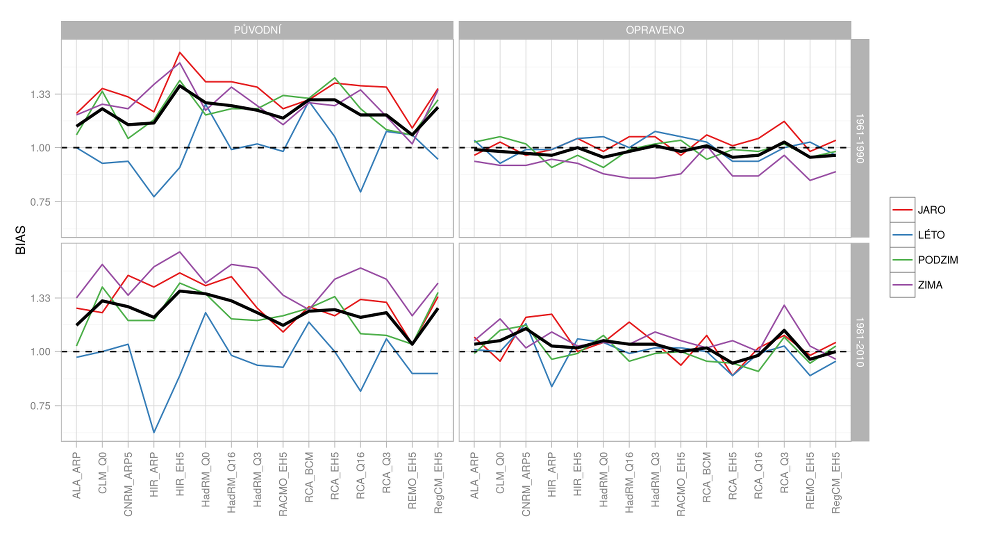
Obr.4.3 Systematická chyba (průměr pro ČR) v maximálním sezónním (barevné čáry) a ročním (tlustá čára) srážkovém úhrnu pro původní a korigovaná data v porovnání s různými pozorovanými obdobími.
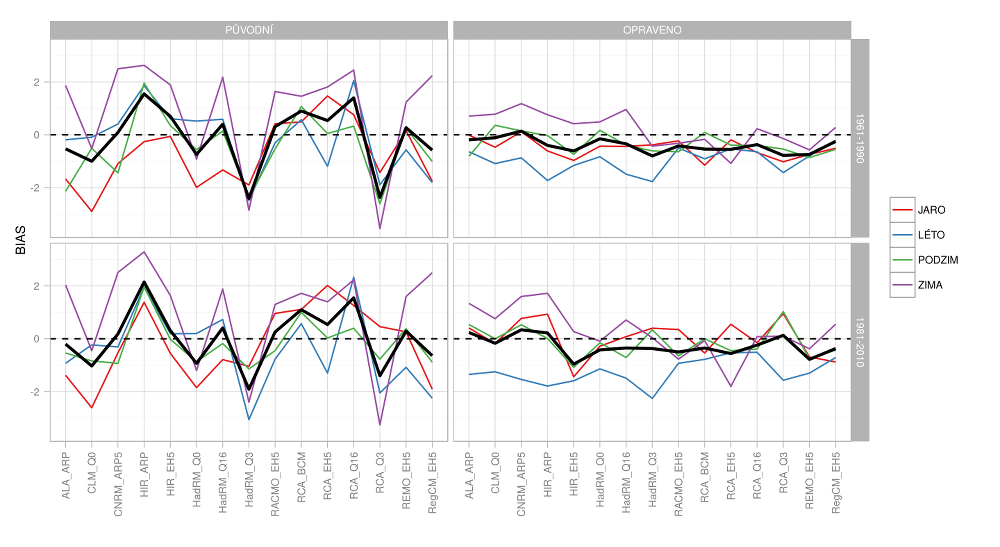
Obr.4.4 Systematická chyba (průměr pro ČR) v maximálním sezónním (barevné čáry) a ročním (tlustá čára) průměrů teploty pro původní a korigovaná data v porovnání s různými pozorovanými obdobími.
4.2 Pokročilá přírůstková metoda - CMIP5 data
Pro tvorbu těchto scénářů byla využita data a R skripty poskytnuté Královským nizozemským meteorologickým institutem (KNMI), viz Kraaijenbrink (2013), které umožňují relativně snadnou aplikaci pokročilé přírůstkové (ADC – Advanced Delta Change) metody (Pelt et al. 2012) na libovolná pozorovaná data srážek a teploty v Evropě. Přírůstková metoda spočívá v transformaci pozorovaných řad tak, aby změna mezi transformovanou a původní časovou řadou odpovídala změně v klimatickém modelu mezi zvolenými obdobími. Nejjednodušší podoba této metody transformuje pouze průměr dané veličiny, nicméně z analýzy mnoha výstupů klimatických modelů je zřejmé, že změny v rozdělení, zejména srážek, jsou komplexnější. ADC metoda umožňuje zahrnout do transformace i změny variability, zjednodušeně tzn., že extrémy se mohou měnit jinak než průměr. Při odvození změn srážek z klimatického modelu ADC metoda uvažuje i systematické chyby simulace. Jelikož teplota je transformována lineárně, nemá systematická chyba na výslednou transformaci teploty vliv.
Srážky jsou transformovány pomocí vztahu
\[ P^* = \begin{cases} a P ^ b & \text{pro $P^O < P^O_{90}$}\\ \frac{\bar{E}^F}{\bar{E}^C} (P^O - P^O_{90}) + a (P^O_{90})^b & \text{pro $P^O > P^O_{90}$}\end{cases} \](4.3)
kde \(P^*\) jsou transformované srážky, \(P\) pozorované srážky, \(P_{90}\) je 90% kvantil srážek, indexy \(^O\), \(^C\) a \(^F\) indikují pozorovaná data, GCM data pro kontrolní období a GCM data pro scénářové období. \(a\) a \(b\) jsou transformační parametry, které jsou odvozeny pro 5denní bloky, což zaručuje sezónní variabilitu změn. Lineární transformace pro hodnoty nad \(P^O_{90}\) zabraňuje výskytu nerealisticky vysokých hodnot, které jsou relativně často výsledkem nelineární transformace pro \(P > P_{90}\) a \(b>1\).
Pro srážky vyšší než 90% kvantil srážek v daném měsíci je vypočtena nadprahová hodnota \(E = P - P_{90}\). Průměrné nadprahové hodnoty v GCM pro kontrolní a scénářové období jsou vypočteny dle
\[\bar{E}^C = \frac{\sum P^C - P^C_{90}}{n^C} \quad \mathrm{a} \quad \bar{E}^F = \frac{\sum P^F - P^F_{90}}{n^F}\](4.4)
kde \(n^C\) a \(n^F\) je počet nadprahových hodnot v kontrolním a scénářovém období. Transformační parametry \(a\) a \(b\) jsou odvozeny z hodnot 60% (\(P_{60}\)) a 90% (\(P_{90}\)) kvantilu srážek dle
\[b = \frac{\log[g_2 P^F_{90}/ (g_1 P^F_{60})] }{\log[g_2 P^C_{90}/ (g_1 P^C_{60})]}\\ a = P^F_{60}/(P^C_{60})^b g_1^{1-b}\](4.5)
kde \(g_1\) a \(g_2\) jsou korekční faktory vyjadřující systematické chyby v \(P_{60}\) a \(P_{90}\) v GCM simulaci pro kontrolní období.
\[g_1 = P^O_{60}/P^C_{60}\] \[g_2 = P^O_{90}/P^C_{90}\](4.6)
Jelikož hodnoty \(P_{60}\), \(P_{90}\), \(\bar{E}^C\) a \(\bar{E}^F\) jsou časově relativně variabilní, jsou průměrné měsíční hodnoty těchto veličin vyhlazeny váženým klouzavým průměrem s váhami 0.25, 0.5 a 0.25. Zároveň hodnota parametru \(b\) i poměru \({\bar{E}^F}/{\bar{E}^C}\) vykazuje značnou prostorovou variabilitu. Tyto parametry jsou proto průměrovány v prostorovém klouzavém okně z pravidelného okolí 8 grid boxů.
Parametry \(a\) a \(b\) byly k dispozici odvozené pro celou Evropu (Kraaijenbrink 2013), přičemž systematické chyby byly spočteny na základě gridovaného E-OBS data setu (Haylock et al. 2008), agregovaného do rozlišení klimatických modelů (tj. cca 150 × 120 km, cca 5 grid boxů relevantních pro ČR, přičemž E-OBS má rozlišení 25 × 25 km). Je známo, že E-OBS je různě kvalitní pro různé části Evropy a že ČR náleží k zemím s relativně malou hustotou dat sloužících k tvorbě E-OBS data setu. Nicméně předpokládáme, že případná systematická chyba, která je zavedená použitím E-OBS dat, je ve srovnání s typickými systematickými chybami klimatických modelů a s přihlédnutím k velikosti GCM grid boxu, do kterého jsou data agregována, zanedbatelná.
Transformace teploty je v ADC metodě prováděna následovně:
\[T^* = \frac{\sigma^F}{\sigma^C} (T - \bar{T}^O) + \bar{T}^O + \bar{T}^F -\bar{T}^C\](4.7)
kde \(T^*\) je transformovaná teplota, \(\bar{T}^O\), \(\bar{T}^C\) a \(\bar{T}^F\) je průměrná měsíční teplota pro pozorovaná data, GCM kontrolní a scénářové období a \(\sigma^C\) a \(\sigma^F\) jsou směrodatné odchylky denní teploty pro kontrolní a scénářové období v GCM.
Odvozené parametry pro GCM z Tab.1.2 byly následně použity k transformaci gridovaných srážek a teploty (Štěpánek et al. 2011) pocházejících z ČHMÚ (viz kapitolu 1.1), kvůli konzistenci s GCM daty bylo uvažováno pouze období 1961–1995. Tato data by samozřejmě mohla být teoreticky použita i pro korekci systematických chyb při odvození transformačních parametrů pro srážky, nicméně to by znamenalo provést celé toto odvození znovu, což nebylo z časových důvodů možné.
Obr. 4.5 ukazuje průběh transformačních parametrů \(a\), \(b\) a \(\bar{E}^F\) a \(\bar{E}^C\) pro různé RCP scénáře a časová období. Parametr \(a\) ovlivňuje průměr srážek. Z jeho hodnot je zřejmé, že v simulacích dochází spíše k růstu srážek v období cca listopad–duben/květen a k jejich poklesu po zbytek roku. Zároveň je patrné zvyšování variability letních srážek (parametr \(b\)) i podílu denních úhrnů vyšších než 90% kvantil.
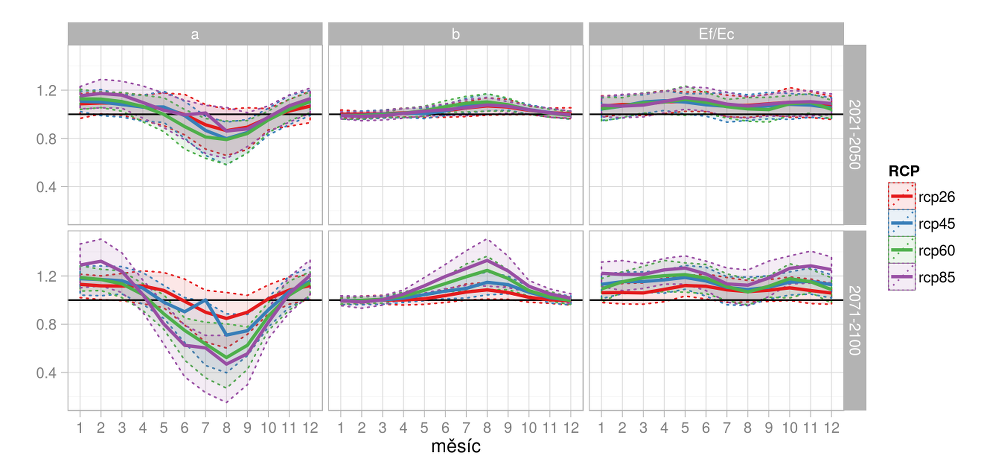
Obr.4.5. Sezónní průběh transformačních parametrů z rovnice 4.3 a různé RCP scénáře a časová období. Tlustá čára znázorňuje medián z GCM simulací pro daný RCP scénář, barevně je vyznačeno mezikvartilové rozpětí.
5 Aplikace scénářů a přehled dopadů
Pro hydrologické modelování byly kromě pozorovaných dat k dispozici dvě sady scénářů změny klimatu, odlišné svou povahou:
pro hydrologické modelování byly kromě pozorovaných dat k dispozici dvě sady scénářů změny klimatu, odlišné svou povahou
pozorované časové řady transformované pomocí ADC metody na základě změn mezi scénářovými obdobími 2021–2050 a 2071–2100 a kontrolním obdobím 1961–1995 pro 191 simulací z projektu CMIP5
Tyto scénářové řady byly použity pro simulaci hydrologické bilance pomocí modelu Bilan s využitím parametrů, které popisuje kapitola 2. Jelikož primárním zájmem bylo odvození změn prvků hydrologické bilance, nikoliv jejich absolutní hodnoty pro jednotlivé roky, pracovali jsme dál s měsíčními, sezónními a ročními změnami vybraných prvků. Jako období, ke kterému jsou změny vztaženy, bylo vybráno období 1981–2010, jednak proto, že lépe vystihuje současné hydroklimatické podmínky a jednak proto, že podobné období je použito i v Páté hodnotící zprávě IPCC (Stocker et al. 2013). Pro ENSEMBLES simulace byly následně spočítány změny průměrů mezi obdobími 1961–1990, 1971–2000, … 2071–2100 a obdobím 1981–2010. Období jsou dále označována i jejich středy, tedy 1975, 1985, … 2085 a kontrolní období 1995. Jelikož pro CMIP5 scénáře byly k dispozici jen změny z období 2035 a 2085 vzhledem k období 1975, bylo pro odvození změn pro chybějící třicetiletá období předpokládáno, že průběh 30letých průměrů mezi průměry dostupnými (1975, 2035 a 2085) je ovlivňován spíše radiačním působením než přirozenou variabilitou tedy, a že je tedy možné hodnotami pro tato období proložit hladkou křivku a z ní odhadnout změny pro všechna ostatní období. Pro každý GCM model, scénář koncentrací RCP a měsíc byly hodnoty průměrů (odtoku, srážek, teploty) interpolovány kubickou spline funkcí. Následně byly spočítány změny podobně jako v případě ENSEMBLES dat.
Přehled dopadů
Na tomto místě se spíše než na podrobnou diskuzi dopadů zaměříme na prezentaci množství dosažených výsledků a konstatování průměrných změn vybraných veličin. Výsledky jsou dále prezentovány v dalších sekcích webu.
Základní přehled modelovaných dopadů změny klimatu v ČR udává Obr. 6.1. Z hlediska historického kontextu modelování dopadů změny klimatu v ČR nejsou tyto (průměrné) výsledky nikterak překvapivé. V souladu s dříve publikovanými výsledky dochází v povodích k růstu zimního odtoku, což je způsobeno částečně zvyšováním zimních srážek a částečně posunem doby tání do dřívějších měsíců, případně omezením tvorby sněhové pokrývky v důsledku zvyšování teploty. V ostatních měsících dochází spíše k snižování celkového i základního odtoku. To je způsobeno vyšší evapotranspirací (důsledek zvýšené teploty), která již není dostatečně kompenzována růstem srážek. Pro scénáře koncentrací RCP6.0 a RCP8.5 dochází navíc ke snižování letních srážek. Průměrné rozsahy změn v uvažovaném souboru simulací uvádí i Tab. 6.1. Průměrné změny byly počítány tak, že nejdříve byl vypočten průměr pro ČR pro každou simulaci klimatického modelu a z těchto průměrů byly poté vypočteny průměrné změny pro jednotlivé scénáře emisí/koncentrací, tzn. rozsahy jsou spočítány z pěti hodnot – tj. 4 RCP + 1 SRES scénář. Počet prvků, z kterých jsou počítány průměry, je různý pro různé scénáře: 1950 A1B, 5850 RCP2.6, 7020 RCP4.5, 3770 RCP6.0, 8190 RCP8.5. Je zřejmé, že v jednotlivých případech (pro jednotlivá povodí a simulace klimatických modelů), mohou být hodnoty změn výrazně mimo rozsah hodnot z tabulky 6.1. Pro zajímavost uvádíme celkové rozsahy změn pro všechna povodí a simulace v Tab. 6.2. Jedná se o jeden z nejjednodušších způsobů vyjádření nejistoty v souboru modelů, který ovšem rozpětí značně nadhodnocuje – např. 20násobné zvýšení zimního základního odtoku lze považovat za nereálné.
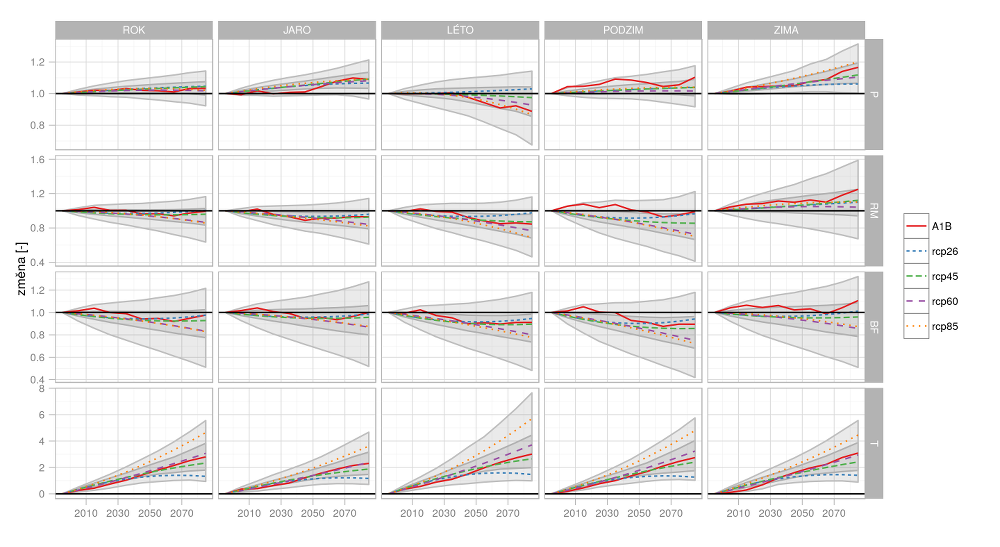
Obr. 6.1 Změny srážek (P), celkového modelovaného odtoku (RM), modelovaného základního odtoku (BF) a teploty (T) pro různé časové horizonty a scénáře emisí/koncentrací (barevné čáry). Šedými polygony jsou vyznačeny oblasti, ve kterých leží 90 % a 75 % všech projekcí. Jedná se o průměry pro ČR.
Tab. 6.1 Rozsah průměrných změn dle jednotlivých scénářů koncentrací pro různá roční období, časové horizonty a veličiny.
| ROK | JARO | LÉTO | PODZIM | ZIMA | |
|---|---|---|---|---|---|
| 2011–2040 | |||||
| P | 1.02 - 1.03 | 1.00 - 1.04 | 1.00 - 1.01 | 1.01 - 1.06 | 1.03 - 1.05 |
| RM | 0.97 - 1.01 | 0.95 - 0.96 | 0.93 - 0.99 | 0.92 - 1.04 | 1.03 - 1.08 |
| BF | 0.95 - 1.00 | 0.96 - 1.01 | 0.93 - 0.97 | 0.91 - 1.00 | 0.97 - 1.04 |
| T | 0.74 - 1.18 | 0.63 - 0.97 | 0.89 - 1.36 | 0.76 - 1.19 | 0.68 - 1.19 |
| 2041–2070 | |||||
| P | 1.02 - 1.04 | 1.04 - 1.07 | 0.94 - 1.02 | 1.02 - 1.07 | 1.05 - 1.12 |
| RM | 0.93 - 0.97 | 0.89 - 0.94 | 0.84 - 0.94 | 0.83 - 0.99 | 1.05 - 1.13 |
| BF | 0.90 - 0.95 | 0.93 - 0.96 | 0.86 - 0.92 | 0.83 - 0.91 | 0.92 - 1.03 |
| T | 1.36 - 2.72 | 1.17 - 2.17 | 1.56 - 3.26 | 1.33 - 2.78 | 1.40 - 2.68 |
| 2071–2100 | |||||
| P | 1.02 - 1.05 | 1.07 - 1.09 | 0.87 - 1.03 | 1.02 - 1.10 | 1.06 - 1.20 |
| RM | 0.86 - 1.00 | 0.82 - 0.96 | 0.69 - 0.98 | 0.70 - 0.99 | 1.04 - 1.25 |
| BF | 0.83 - 0.98 | 0.87 - 1.00 | 0.78 - 0.95 | 0.72 - 0.94 | 0.86 - 1.11 |
| T | 1.33 - 4.64 | 1.17 - 3.62 | 1.47 - 5.70 | 1.27 - 4.80 | 1.40 - 4.46 |
Tab. 6.2 Rozsah změn z jednotlivých simulací a povodí, pro různá roční období, časové horizonty a veličiny.
| ROK | JARO | LÉTO | PODZIM | ZIMA | |
|---|---|---|---|---|---|
| 2011–2040 | |||||
| P | 0.93 - 1.16 | 0.81 - 1.26 | 0.79 - 1.31 | 0.87 - 1.33 | 0.76 - 1.28 |
| RM | 0.57 - 1.73 | 0.51 - 1.67 | 0.51 - 1.96 | 0.25 - 4.60 | 0.39 - 2.57 |
| BF | 0.44 - 2.35 | 0.42 - 2.07 | 0.25 - 3.47 | 0.07 - 9.69 | 0.32 - 5.62 |
| T | 0.18 - 1.99 | -0.28 - 2.00 | 0.07 - 2.62 | 0.01 - 1.74 | -0.16 - 2.14 |
| 2041–2070 | |||||
| P | 0.80 - 1.22 | 0.8.5 - 1.37 | 0.60 - 1.28 | 0.78 - 1.39 | 0.70 - 1.35 |
| RM | 0.29 - 2.07 | 0.37 - 1.97 | 0.24 - 1.86 | -0.06 - 5.29 | 0.17 - 2.75 |
| BF | 0.13 - 2.37 | 0.17 - 2.13 | 0.11 - 3.29 | -0.10 - 5.40 | 0.01 - 9.07 |
| T | 0.35 - 4.17 | 0.30 - 3.57 | 0.36 - 5.67 | 0.28 - 3.82 | 0.38 - 4.18 |
| 2071–2100 | |||||
| P | 0.74 - 1.29 | 0.78 - 1.48 | 0.51 - 1.38 | 0.74 - 1.49 | 0.87 - 1.61 |
| RM | 0.20 - 2.38 | 0.24 - 2.28 | 0.16 - 2.34 | 0.02 - 4.89 | 0.09 - 5.37 |
| BF | 0.10 - 3.66 | 0.10 - 2.99 | 0.05 - 3.24 | 0.01 - 7.59 | 0.01 - 18.83 |
| T | 0.16 - 6.71 | 0.13 - 5.86 | -0.03 - 9.28 | -0.32 - 6.87 | 0.30 - 6.80 |
Literatura
BERAN, A, M PELÁKOVÁ, L KAŠPÁREK, M HANEL a R KOŽÍN, 2014. Výpočet velikosti dotace podzemních vod za pomoci hydrologického modelování na vybraných hydrogeologických rajonech ČR. VTEI. roč. 56, č. 4.
BERAN, A., S. HORÁČEK a M. HANEL, 2011. Zjednodušení metody výpočtu potenciální evapotranspirace v nové verzi modelu BILAN. VTEI. roč. 53, č. mimořádné číslo III, s. 15–18.
COLLINS, Matthew, Ben BOOTH, Glen HARRIS, James MURPHY, David SEXTON a Mark WEBB, 2006. Towards quantifying uncertainty in transient climate change. Climate Dynamics. B.m.: Springer Berlin / Heidelberg, roč. 27, č. 2, s. 127–147.
EHRET, U, E ZEHE, V WULFMEYER, K WARRACH-SAGI a J LIEBERT, 2012. HESS opinions„ should we apply bias correction to global and regional climate model data?" Hydrology and Earth System Sciences Discussions. B.m.: Copernicus GmbH, roč. 9, č. 4, s. 5355–5387.
GUDMUNDSSON, L, JB BREMNES, JE HAUGEN a T ENGEN-SKAUGEN, 2012. Technical note: Downscaling rCM precipitation to the station scale using statistical transformations–a comparison of methods. Hydrology and Earth System Sciences. B.m.: Copernicus GmbH, roč. 16, č. 9, s. 3383–3390.
HAERTER, JO, S HAGEMANN, C MOSELEY a C PIANI, 2011. Climate model bias correction and the role of timescales. Hydrology and Earth System Sciences. B.m.: Copernicus GmbH, roč. 15, č. 3, s. 1065–1079.
HAYLOCK, M, N HOFSTRA a A KLEIN-TANK, 2008. A european daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. Journal of Geophysical Research. roč. 113, č. D20, s. D20119.
HEWITT, C. D. a D. J. GRIGGS, 2004. Ensembles-based Predictions of Climate Changes and their Impacts. Eos. roč. 85, č., s. 566.
HORÁČEK, S., O. RAKOVEC, L. KAŠPÁREK a A. VIZINA, 2009. Vývoj modelu hydrologické bilance BILAN. VTEI. roč. 51, č. mimořádné číslo I, s. 2–5.
KAŠPÁREK, L, 1989. Odhad směrodatné chyby průtoků a jejich základních charakteristik. B.m.: Český hydrometeorologický ústav.
KAŠPÁREK, L, JV DATEL, M HANEL, A HRABÁNKOVÁ a M KNĚŽEK, 2012. Rebilance zásob podzemních vod: Metodika stanovení průměrné hodnoty přírodních zdrojů podzemních vod kvartérních hydrogeologických rajonů. B.m.: Výzkumný ústav vodohospodářský T. G. Masaryka, v.v.i.
KAŠPÁREK, L, R NAAROVÁ a Špalle M, 2000. Hodnocení a modelování srážko-odtokových vlastností povodí. B.m.: Výzkumný ústav vodohospodářský T. G. Masaryka, v.v.i.
KRAAIJENBRINK, Philip, 2013. Advanced delta change method. B.m.: KNMI.
KRÁSNÝ, J, M KNĚŽEK, A ŠUBOVÁ, H DAŇKOVÁ, M MATUŠKA a V HANZEL, 1982. Odtok podzemní vody na území Československa. Praha: ČMÚ v SNTL.
MÁCA, P, S HORÁČEK a A VIZINA, 2013. Optimalizace parametrů modelu bilan metodou sCDE. 2013.
OUDIN, Ludovic, Lætitia MOULIN, Hocine BENDJOUDI a Pierre RIBSTEIN, 2010. Estimating potential evapotranspiration without continuous daily data: possible errors and impact on water balance simulations. Hydrological Sciences Journal. roč. 55, č. 2, s. 209–222.
PELT, S. J. van, J. BEERSMA a T. A. BUISHAND, 2012. Future changes in extreme precipitation in the Rhine basin based on global and regional climate model simulations. Hydrology and Earth System Sciences. roč. 16, č., s. 4517–4530.
REIFEN, C. a R. TOUMI, 2009. Climate projections: Past performance no guarantee of future skill? Geophys. Res. Lett. roč. 36, č. L13704.
STOCKER, Thomas F, Dahe QIN, Gian-Kasper PLATTNER, M TIGNOR, Simon K ALLEN, Judith BOSCHUNG, Alexander NAUELS, Yu XIA, Vincent BEX a Pauline M MIDGLEY, 2013. Climate change 2013: The physical science basis. B.m.: Intergovernmental Panel on Climate Change, Working Group I Contribution to the IPCC Fifth Assessment Report (AR5)(Cambridge Univ Press, New York).
ŠTĚPÁNEK, P, P ZAHRADNÍČEK a R HUTH, 2011. Interpolation techniques used for data quality control and calculation of technical series: an example of a Central European daily time series. IDÖJÁRÁS - Quarterly Journal of the Hungarian Meteorological Service. roč. 115, č. 1–2, s. 87–98.
Dopady klimatické změny na hydrologické poměry v povodích ČR
Soubor specializovaných map
Martin Hanel, Stanislav Horáček, Ondřej Ledvinka, Martin Tomek, Radim Tolasz, Martin Stříž, Jan Daňhelka, Kateřina Hánová
Soubor map znázorňuje odhady možných změn sezónních a ročních průměrů hydrometeorologických veličin způsobené klimatickou změnou pro 130 povodí pokrývajících Českou republiku, přičemž syntetizuje simulované změny dle rozsáhlého souboru simulací klimatických modelů (cca 200), včetně simulací, které sloužily k přípravě podkladů pro Pátou hodnotící zprávu Mezivládního panelu pro klimatickou změnu (IPCC AR5), tzv. CMIP5 souboru modelů. Mapy zobrazují změny srážek (P), teploty (T), potenciální evapotranspirace (PET), územního výparu (E), celkového odtoku (RM), základního odtoku (BF), 95% kvantilu z čáry překročení měsíčního celkového (RM95) a základního odtoku (BF95) a baseflow indexu (tj. poměr základního a celkového odtoku, BFI).
Tento soubor map je svým plošným a časovým rozsahem, množstvím a aktuálností modelovaných scénářů změny klimatu a snadnou dostupností prostřednictvím webové aplikace v České republice jedinečný a jako takový může najít uplatnění v širokém spektru aplikací souvisejících s dlouhodobým plánováním vodních zdrojů, využití území, energetiky apod.
Soubor map slouží jako indikátor (prostorově) průměrných změn pro jednotlivá povodí z definované sady (jako celků). Zatímco pro srážky a teplotu není vzhledem k celkovým nejistotám odhadů nutné uvažovat prostorovou variabilitu změn v rámci těchto povodí, v případě hydrologických veličin nelze jednoduše očekávat, že by odhadované změny byly distribuovány rovnoměrně do jednotlivých dílčích povodí. Zde je potřeba výsledky interpretovat s využitím znalostí místního hydrologického režimu a současných trendů a případných problémů.
Odhad charakteru budoucího klimatu je zatížen značnou nejistotou pramenící z nejistého socio-ekonomického vývoje společnosti, nedostatečnou schopností modelovat klima a z přirozené variability klimatických veličin. Prezentované mapy proto neudávají v případě jedné veličiny pro jedno povodí, časový horizont a roční období jednu hodnotu změny, ale zobrazují změny pro různé modely a scénáře.
Soubor map vznikl v souvislosti s řešením výzkumného projektu TA02020320 Podpora dlouhodobého plánování a návrhu adaptačních opatření v oblasti vodního hospodářství v kontextu změn klimatu spolufinancovaného Technologickou agenturou České republiky.