Scénáře změny klimatu

Kvůli systematickým chybám je přímé použití výstupů klimatických modelů pro modelování dopadů změny klimatu v současnosti vyloučeno. Další překážkou přímé aplikace výstupů klimatických modelů je často nesoulad měřítka klimatických modelů (výpočetní síť desítky až stovky kilometrů) s měřítkem požadovaným (bod – stanice, omezená plocha povodí a pod.).

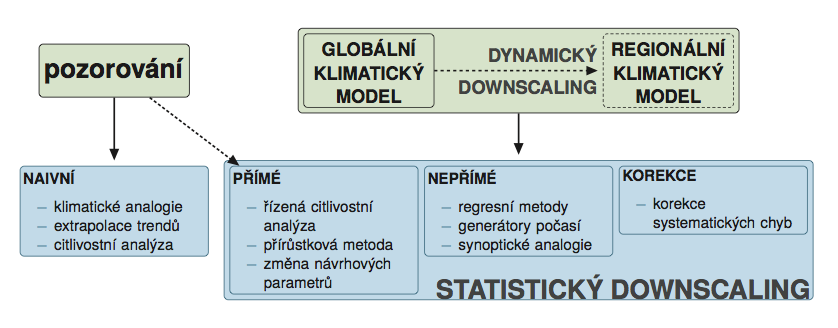
Pro tvorbu scénářů změn klimatu je možno použít řadu metod. Tyto metody lze dle nároků na data rozdělit na metody nevyžadující informace z klimatických modelů (viz Obr. 2.1), naivní metody – (viz Box 2.1), na metody založené na transformaci pozorovaných dat s využitím poznatků odvozených ze simulací klimatických modelů, přímé metody – (viz Box 2.2), metody využívající generátory počasí, regresní modely apod. nepřímé metody – (viz Box 2.3) a metody využívající transformované simulace klimatických modelů – (viz Box 2.4). Jednotlivé metody se liší zejména množstvím předpokladů, které na změny klimatu kladou a výpočetní a odbornou náročností. Je proto evidentní, že neexistuje jedna „správná“ metodika tvorby scénářů změn klimatu, ale jejich použití se vždy řídí účelem jejich aplikace.

Obr. 2.1 Rozdělení metod tvorby scénářů změny klimatu.

U všech metod lze identifikovat klady i zápory, nicméně hlavním limitem použití pokročilých metod je zpravidla nedostatek pozorovaných dat, jež jsou nezbytná pro kalibraci jednotlivých postupů. Navíc tyto metody většinou vyžadují speciální znalosti, programové vybavení apod. a není tedy vždy schůdné je aplikovat v běžné vodohospodářské praxi.  Volba vhodné metodiky pro tvorbu scénářů je klíčová při modelování dopadů změny klimatu.

Všechny známé a dostupné metody zahrnují předpoklady stacionarity systematické chyby, variability apod. Současně je rovněž předpokládána platnost kalibrace a schematu hydrologického modelu. Uvedené předpoklady však nejsou naplněny, navíc není zaručeno, že při aplikaci různých postupů nepůsobí stejným směrem. Je proto třeba být si vědomi těchto nenaplněných předpokladů při interpretaci výsledků.

Mezi zásadní požadavky na scénář změny klimatu, které uvádí např. (Smith a Hulme 1998) patří:

• Scénáře by měly být konzistentní s obecně přijímaným rozpětím změn (tj. neměly by, není-li k tomu nějaký zvláštní důvod, předpokládat oteplení o 10°C apod.).

• Scénáře by měly být fyzikálně věrohodné, tj. například by neměly předpokládat, že změny srážek budou na celém kontinentě konstantní. Zároveň by změny veličin měly být navzájem konzistentní, např. rostoucí srážkové úhrny by měly být doprovázeny větší oblačností apod.

• Scénáře by se měly zabývat všemi veličinami vstupujícími do modelu dopadů v odpovídajícím prostorovém a časovém rozlišení. Hydrologické modely např. často pracují se srážkami, teplotou a potenciální evapotranspirací. Všechny tyto veličiny by proto měly být součásti scénáře změny klimatu.

O vhodnosti metody lze tedy rozhodnout vždy pouze v kontextu konkrétní aplikace. Nejdůležitější faktory, které je potřeba zohlednit při volbě scénáře změn klimatu jsou časové a prostorové měřítko.

Časové měřítko

Časové měřítko pro scénáře změny klimatu je zpravidla dáno časovým měřítkem modelu posuzovaného systému pro současné podmínky. Ve většině případů probíhá modelování v denním či měsíčním kroku pro některé problémy je nutné uvažovat časový krok kratší (např. hodinový). Podobně, většina uvedených metod tvorby scénářů je nejčastěji aplikována na denní případně měsíční data. To je zároveň časové rozlišení, které umožňuje využití výstupů klimatických modelů (zpravidla dostupné v denním kroku).

Měsíční a delší časové měřítko je typické pro řešení změn celkové vodní bilance, zabezpečenosti zásobování vodou a charakteristik sucha. Typickou metodou používanou v ČR je jednoduchá přírůstková metoda, popřípadě citlivostní analýza, často zkoumající reakci systémů na určité oteplení. Tato časová měřítka jsou i typickým uplatněním analogových metod a extrapolací trendu.

Pro denní a vícedenní časové měřítka, která jsou relevantní pro vyhodnocení regionálních povodní (plocha povodí větší než cca 30 000–50 000 km²), hydroenergetiku či hodnocení kvality vody, se zpravidla využívá korekce systematických chyb nebo přírůstkové metody zahrnující korekce/změny průměrů i variability. Rovněž nepřímé metody jsou zpravidla aplikovány v denním kroku.

Modelování v krátkém časovém kroku je typické pro problematiku městské hydrologie, eroze, (přívalových) povodní apod. Z hlediska scénářů změn klimatu je tato oblast metodicky problematická, především proto, že vliv klimatické změny na charakteristiky krátkodobých srážek je značně nejistý. Metody tvorby scénářů uplatňované v případě krátkodobých srážek zpravidla využívají scénáře v denním kroku, které poté disagregují do hodinových či kratších rozlišení, časté je využití generátorů počasí.

Prostorové měřítko

Typický zdroj informací pro scénáře změny klimatu – klimatické modely – pracují v prostorovém rozlišení v řádu jednotek až desítek (regionální klimatické modely) popřípadě desítek až stovek (globální klimatické modely) km. Výstupy klimatických modelů je nutné chápat jako prostorové průměry nikoliv bodové hodnoty. To má zásadní vliv např. na srážkové extrémy (výška n-leté srážky se snižuje s velikostí zasažené plochy) nebo na teplotu (zejména v členitém terénu může být teplota značně odlišná i při relativně malé horizontální vzdálenosti). Přístup k datům z klimatických modelů při tvorbě scénářů klimatické změny se liší dle toho zda je scénář vytvářen pro bod nebo plochu.

Bodové scénáře na základě výstupů klimatických modelů jsou nejčastěji vytvářeny pomocí

• delta metody: Zpravidla se předpokládá, že změny v daném bodě jsou stejné jako změny v příslušné výpočetní buňce klimatického modelu – tzn. přírůstkové faktory jsou odvozeny na úrovni výpočetních buněk klimatického modelu a následně použity pro transformaci bodových dat. To mimo jiné znamená, že vztah mezi plošnou a bodovou informací v pozorovaných datech by měl být lineární. Zároveň je třeba mít na paměti, že změny veličin mohou záviset například na nadmořské výšce. Nicméně vzhledem k ostatním nejistotám, se zmíněné zjednodušení dá pokládat za přijatelné, zejména pokud jsou pro odvození bodových scénářů použity výstupy regionálních klimatických modelů.

• korekce systematických chyb: I v tomto případě se nabízí zjednodušení pomocí zahrnutí transformace z plošných dat na data bodová přímo do korekční funkce. Prakticky to znamená, že korekční funkce je hledána na základě porovnání výstupu klimatického modelu s pozorovanými bodovými daty.

• regresních metod: Standardně jsou dávány do vztahu výstupy klimatického modelu s bodovými veličinami.

Plošné scénáře je možno chápat buď jako scénáře pro prostorové průměry vybraných veličin (např. časové řady průměrných srážek a teploty na vybrané povodí) nebo jako prostorově distribuované scénáře.

Strategie tvorby scénářů změny klimatu pro prostorové průměry se odvíjí od velikosti uvažované plochy v porovnání s rozlišením klimatického modelu. V případě, že uvažovaná plocha je podstatně menší než plocha výpočetní buňky klimatického modelu, je možno postupovat jako v případě scénářů bodových. V případě, že zájmová plocha je srovnatelná či větší než výpočetní buňka klimatického modelu, jsou pro tvorbu scénáře zpravidla využívány informace ze všech relevantních výpočetních buněk klimatického modelu. Zpravidla je nejprve vypočten prostorový průměr ze simulace klimatického modelu. Tento průměr je následovně korigován nebo využit pro přírůstkovou metodu. Možný je i obrácený postup, kdy korekce nebo odvození a aplikace přírůstkových faktorů probíhá na úrovni jednotlivých výpočetních bodů a plošný průměr je vypočten až poté. Druhý postup je možno považovat za správnější (umožňuje nelineární transformace vztahů v ploše povodí), na druhé straně jsou pro jeho aplikaci nezbytná pozorovaná data ve stejné výpočetní síti jako v případě uvažovaného klimatického modelu.

Prostorově distribuované scénáře v rozlišení klimatického modelu je možno jednoduše získat aplikací korekce systematických chyb či delta metody na jednotlivé výpočetní buňky. V případě potřeby scénářů v podrobnějším měřítku je možno použít prostorové interpolační metody, zpravidla v kombinaci s předpokladem neměnnosti prostorové struktury daných veličin.