Vybrané metody používané k transformaci časových řad při tvorbě scénářů
Při modelování dopadů změn klimatu se uplatňují metody vycházející z transformace časových řad, ať už v rámci korekce systematických chyb nebo v případě přírůstkové metody. Používané transformace lze shrnout do několika skupin (Teutschbein a Seibert, 2010), jenž jsou rozebrány níže.
Prahové hodnoty
Jde o úpravu četnosti dní se srážkami, jež je obecně v klimatických modelech zpravidla větší než v pozorování v důsledku tzv. drizzling efektu, který spočívá v simulace velkého počtu dní s velmi malými srážkovými úhrny. Často je pak simulovaná řada srážek upravena tak, že hodnoty srážek pod určitým prahem (např. 0,1 mm) jsou nahrazeny nulovou srážkou. Korekce či změna četnosti dní se srážkami může být nicméně komplikovanější, zejména je-li nutné četnost zvyšovat.
Jednoduché transformace
Spočívá v úpravě měsíčních průměrů (zpravidla srážek – P a teploty – T, případně relativní vlhkosti vzduchu – H [%]). Úprava probíhá ve dvou krocích:
- Odvození transformačních faktorů:
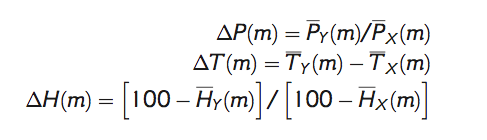
(2.2)
- a transformace časový řad:
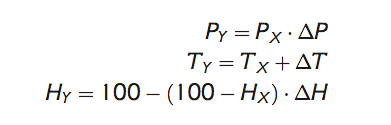
(2.3)
kde m je měsíc x (T,P) je průměr veličiny x (T,P) a symboly X a Y značí při odvozování parametrů transformace simulovaná data pro kontrolní a scénářové období v případě přírůstkové metody a simulovaná a pozorovaná data pro kontrolní období v případě korekce systematických chyb. Při transformaci pak X odpovídá pozorovaným datům pro kontrolní období v případě přírůstkové metody a simulaci klimatického modelu pro budoucí období pro korekci systematických chyb (viz Tabulka 2.2). Nevýhodou této transformace je zejména, že ovlivňuje pouze průměr daných veličin.
Tab. 2.2 Přehled dat použitých pro odvození transformačních parametrů a následnou transformaci
| Odvození parametrů X |
Y | Transformace X |
Y | |
|---|---|---|---|---|
| Přírůstková metoda | simulace pro kontrolní období | simulace pro scénářové období | pozorování | scénářová řada |
| Korekce systematických chyb | simulace pro kontrolní období | pozorování | simulace pro | scénářová řada |
Transformace zahrnující variabilitu
Jelikož jak chyby, tak změny srážek, teploty i relativní vlhkosti vzduchu se týkají jak průměrů, tak variability, je zpravidla vhodné uvažovat pokročilé transformace ovlivňující vyšší momenty statistického rozdělení uvažovaných veličin. Pokročilé transformace je rovněž doporučeno používat v případě modelování dopadů změn klimatu v kratším než měsíčním časovém kroku. Pro srážky (P) a relativní vlhkost vzduchu (H) je typicky využito nelineární transformace
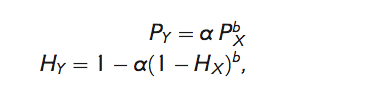
(2.4)
pro teplotu je využívána lineární transformace
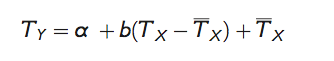
(2.5)
kde a a b jsou parametry transformace pro jednotlivé měsíce či dny a význam symbolů X a Y je stejný jako v Tabulce 5.2. V případě srážek a relativní vlhkosti je nejprve optimalizována hodnota parametru b tak, aby cv(PY) = cv(PbX ), respektive cv(1 − HY) = cv[(1 − HX)b], kde cv je koeficient variace. Následně je vypočítána hodnota parametru α, jako poměr PY/PbX, respektive (1 − HY)/(1 − H)X. V případě teploty jsou parametry α a b odvozeny přímo z rozdílu průměrů, respektive podílu směrodatných odchylek (sd) teploty, tedy a = TY − TX, b = sd(TY)/sd(TX).
Jelikož nelze předpokládat, že by změny byly během roku konstantní, jsou parametry a a b pro všechny veličiny odvozeny buď zvlášť pro každý měsíc nebo pro každý den roku (viz Shabalova et al., 2003; Leander a Buishand, 2007) z časového okna zahrnujícího předcházejících a následujících 30 kalendářních dní ze všech let v uvažovaném období (tedy např. v případě 9. 4. a období 1961–1990 jsou parametry a a b odhadovány z dat zahrnující časové okno 10. 3.–9. 5. pro roky 1961, 1962, …, 1990), Obr.2.4 udává odhady parametrů a a b pro dvě simulace regionálních klimatických modelů.
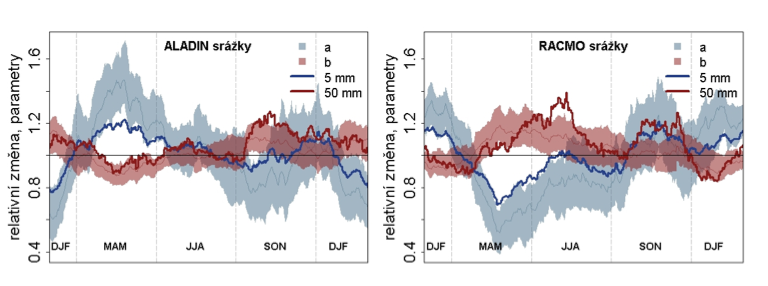
Obr. 2.4 Transformační parametry a a b pro srážky dle regionálních klimatických modelů ALADIN-CLIMATE/CZ a RACMO. Barevné polygony ukazují parametry pro daný den, rozpětí je pro výpočetní buňky pokrývající ČR. Modrá a červená čára odpovídá změně kvantilů srážek odpovídajících úhrnu 5 mm a 50 mm.
Transfer distribuční funkce
Tato metoda (v literatuře označovaná mnoha termíny – např. kvantilová metoda, mapování kvantilů, mapování pravděpodobností, vyrovnání histogramů) spočívá v odvození transferové funkce, jež zaručuje, že hodnoty transformované řady odpovídají stejným kvantilům jako příslušné hodnoty řady původní. Metoda se nejčastěji používá pro korekci systematických chyb, nicméně je možné ji aplikovat i pro transformaci pozorovaných dat v rámci přírůstkové metody, někdy jsou obě metody zkombinovány – tj. nejprve je aplikována korekce systematických chyb a korigovaná řada je pak použita jako podklad pro přírůstkovou metodu.
Formálně lze korekci rozdělení pravděpodobnosti simulované veličiny Pm (např. srážek simulovaných klimatickým modelem) pomocí rozdělení pozorované veličiny Po (např. pozorované srážky) zapsat jako transformaci
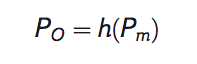
(2.6)
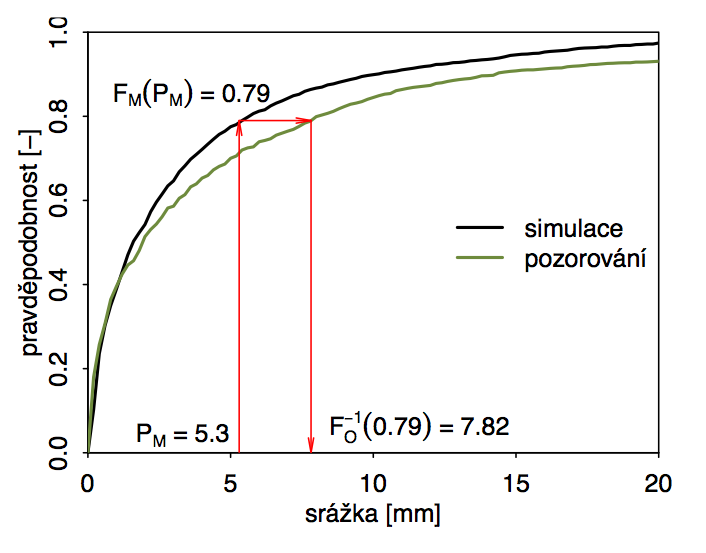
Obr. 2.5 Demonstrace využití mapování kvantilů při korekci systematických chyb v rozdělení srážek. Čáry ukazují distribuční funkce nenulových srážek pro simulovaná a pozorovaná data. Symboly viz text. Ukázaná je korekce simulované srážky o velikosti 5.3 mm, která odpovídá 79% kvantilu simulovaných srážek. Korigovaná hodnota je nalezena jako 79% kvantil pozorovaných srážek, tedy 7.82 mm.
Transformované rozdělení h(Pm) je pak stejné jako rozdělení pozorované veličiny. Transformace h je odvozena pomocí tzv. probability integral transformation, tj. je využito toho, že distribuční funkce libovolné spojité veličiny má rovnoměrné rozdělení. Transformace má pak podobu
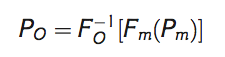
(2.7)
kde Fm je (empirická) distribuční funkce simulovaných dat a F−10 je kvantilová funkce pozorovaných řad. Zjednodušeně se dá postup popsat tak, že nejprve je zjištěna pravděpodobnost dosažení simulované srážky a následně je za ni dosazena hodnota z pozorovaných dat se stejnou pravděpodobností.